Mindannyiunk életében alapvető fontosságú, hogy milyen a partnerünk, családtagjaink, barátaink és ismerőseink által alkotott szociális kapcsolatrendszer. Ebben a szociális erőtérben éljük le életünket, melytől megfosztva, Robinson Crusoe-ként „csupasz majmok” sem lennénk, hiszen a majomfajok legnagyobb részének egyedeit is kiterjedt és bonyolult szociális viszonyrendszer köti össze. Az ember szociális voltának gyökereit mélyen a biológiában fedezhetjük fel. Több érdekes, biológiai és szociológiai jellemzőket összekapcsoló megfigyelés utal erre. Ismert például, hogy az emberszabású majmok agymérete és a csoportméret erős korrelációt mutat. Az emberek általában hatékonyabban oldanak meg egyszerű logikai feladatokat, ha azok a szociális viszonyok nyelvén vannak megfogalmazva (kivéve pl. az autistákat, akiknek egyik közös jellemzőjük a csökkent szociális képesség). A social animal kifejezés nem csak állandóan bulizó embertársainkra vonatkoztatható, hanem emberi mivoltunk egyik leglényegesebb tulajdonságát fejezi ki.

Szociológia és hálózatelmélet

A társadalomtudományok értelemszerűen az emberi társadalom különböző vetületeivel foglalkoznak; közülük a szociológia az, amelynek legáltalánosabb célja a társadalom struktúrájának és folyamatainak megértése, a társadalmi rendszerek kialakulásának és folyamatos dinamikájának kutatása. A mai szociológia – sok egyéb társadalomtudományhoz hasonlóan – gyakran megelégszik egyfajta leíró hozzáállással anélkül, hogy explicit modelleket vezetne be. Természetesen egy újonnan szemügyre vett társadalom, csoport vagy esemény tanulmányozásakor a szociológus is valamiféle modellt használ, melyek alapján következtéseket von le. Ennek a rejtett modellezésnek azonban megvan az a tulajdonsága, hogy minden kutatónak kicsit más modelljei lesznek, de a vitákban és a publikációkban csak a következtetések jelennek meg, az azokhoz vezető implicit modellek közvetlenül nem ütköznek egymással.

Itt rögtön le kell szögeznünk, hogy az explicit modellezést a szociológiának nem arról a leginkább értelmezőnek nevezhető részterületéről hiányoljuk, amely a nagyléptékű társadalmi folyamatokat vizsgálja, gyakran történelmi vagy kultúrantropológiai eszközökkel. Vizsgálódásunk tárgyát leszűkítjük a társadalmi kapcsolatrendszer szerkezetére, s azt az egyszerűnek hangzó kérdést tesszük fel, hogy milyen általános törvényszerűségek hozzák létre, határozzák meg a fent említett szociális erőteret. Persze könnyen találhatunk kiragadott példát jól definiálható, fontos kapcsolatokra, mint például a rokoni vagy munkahelyi kapcsolatok, de az alapvető kérdés az: vajon megadható-e kapcsolattípusok egy olyan listája és statisztikus eloszlása, ami alapján azt állíthatjuk, hogy nagyjából megragadtuk a szociális hálózat egészét, azaz tudjuk-e jól modellezni a szociális hálózatot?

Cikkünk témája az az új és izgalmas megközelítés, amely a szociológia, a közgazdaságtan és a hálózattudomány határmezsgyéjén mozogva azt a célt tűzi maga elé, hogy a társadalmi kapcsolatrendszerek vizsgálata során felmerülő, általánosan megfogalmazható kérdésekre explicit modellezés segítségével adjon választ, s feltárja a modellhálózatok egyszerű, könnyen leírható szabályszerűségeit. A társadalomtudós legkomolyabb kritikája az ilyen interdiszciplináris kutatással szemben az lehet, hogy az explicit modellezés szükségszerű velejárója a drasztikus egyszerűsítés. Nehéz elfogadnia, hogy ha egy szociális kapcsolatrendszert történetesen egy pontokkal és az azokat összekötő éleket tartalmazó hálóval modellezünk, akkor nem veszítünk el azonnal minden jogot arra, hogy a valódi társadalomról, tehát emberekről, családokról, városokról tegyünk állításokat. Az egyszerűsítés azonban nem önmagáért való, nem csupán a modellépítő kutató kényelmét szolgálja, hanem magában hordozza a predikció lehetőségét. Ha a modellünk elég egyszerű ahhoz, hogy ne veszítse érvényét új helyzetekben, akkor vizsgálataink eredményeit alkalmazhatjuk más, eddig még nem vizsgált rendszerekre is. Természetesen itt egy finom egyensúlyról van szó: minél egyszerűbb egy modell, annál többféle helyzetben használható, de ugyanakkor annál pontatlanabbul, annál elnagyoltabban írja le a vizsgált rendszert. Az alábbiakban részletezett interdiszciplináris kutatómunka jelentősége abban áll, hogy a szokványosnál merészebben egyszerűsít a társadalom modellezésében, abban a reményben, hogy ez később hasznos predikciókhoz vezet.

Mindenképpen figyelemre méltó, hogy a társadalom modellezésének eme absztrakt formája nem csökkenti, hanem éppen hogy növeli az érdeklődést a téma irányában. Erről tanúskodik, hogy az utóbbi években a média mennyire felkapta a hálózatok kutatásával kapcsolatos egészen egyszerű mérési próbálkozásokat, legyenek azok kapcsolatosak a világháló lapjai közötti kattintások számával vagy az embereket egymással összekötő ismerősi lánc hosszával. Úgy tűnik, ezek a kérdések mindenkit izgatnak, pedig látszólag semmi hasznos nincs abban, ha megtudjuk, hogy hány kézfogásnyira vagyunk az amerikai elnöktől – feltéve, hogy ez több mint kettő. Talán arról lehet szó, hogy mindenki nap mint nap tapasztalja, hogy mennyire fontos szerepet játszik életében, hogy kiket ismer: nemcsak pletykák terjednek az ismerősök hálóján keresztül, hanem gyakran állásajánlatok, fogyasztói szokások, az üzletkötés és párkapcsolat-teremtés lehetősége is. Elvontabb értelemben talán a globalizálódó társadalom egyfajta önreflexiós igényét is kielégíti e téma tárgyalása, felszínen tartása.

A hálózattudomány fogalmai

A hálózatok vizsgálatának kezdete Leonhard Euler német matematikus munkásságához köthető. A történet szerint Euler lakóhelyét, Königsberg városát szerette volna bebarangolni úgy, hogy mind a hét hídon pontosan egyszer megy át. A problémát úgy fordította le absztrakt kérdéssé, hogy Königsberg különböző városrészeit pontokkal, az azokat összekötő hidakat szakaszokkal ábrázolta, s így a tudománytörténet első absztrakt hálózatához jutott. Ezen ábrázolás segítségével azután meggyőződött arról, hogy a kívánt út nem létezik; ugyanakkor általánosan is megválaszolta azt a kérdést, hogy milyen hálózatok esetében lehetséges az ilyen bejárás (amelyet azóta Euler-bejárásnak nevezünk). Hasonló, a hálózatok nyelvén egyszerűen megfogalmazható problémák ma is nagy gyakorlati fontossággal bírnak a különböző szaktudományokban. Ha például a feladatot megfordítjuk, vagyis az a célunk, hogy minden pontot pontosan egyszer látogassunk meg, a Hamilton-bejárást kapjuk. Nagyon sok optimalizációs probléma lefordítható az ún. „utazó ügynök”-problémára, ahol egy minden pontot érintő bejárás teljes hosszát akarjuk minimalizálni (hiszen az utazó ügynök szeretne minél hamarabb hazaérni). De említhetjük az elvágás problémáját is: hány élt kell legalább elvágnunk ahhoz, hogy egy adott háló kettő (vagy több) részre essen szét?

Társadalmi hálókról beszélünk, ha egy adott társadalmi csoport vagy réteg aktorait (szereplőit) tekintjük a hálózat pontjainak, és két pontot éllel (szakasszal) kötünk össze, amennyiben a két aktor között fennáll egy általunk fontosnak tartott kapcsolat. Például egy ismeretségi háló pontjai egyes emberek, élei pedig két ember ismeretségét reprezentálják. Egy ilyen egyszerű, pontokból és élekből álló absztrakt hálózat azonban ritkán írja le hűen a valóságot. Egy ismeretség ugyanis lehet erős vagy gyenge, időszakos vagy hosszantartó, kölcsönös vagy egyirányú, egyenlők közötti vagy alárendelt viszonyon alapuló és így tovább. Egyik megoldás a bonyolultabb lehetőségek leírására, hogy irányított, súlyozott hálót használunk, amelyben minden élnek iránya van, és számokat, ún. súlyokat is rendelünk hozzájuk attól függően, hogy az adott kapcsolat mennyire játszik fontos szerepet a hálózatban. A telefonhívások rendszerét például, mely a valódi ismeretségek hálójának egyfajta közelítése, egy irányított (hiszen minden hívást valamely fél kezdeményez) és a hívások számával súlyozott hálózat írja le. További probléma azonban, hogy a társadalmi kapcsolatok ritkán jellemezhetők konkrét számokkal. Ilyenkor szerencsésebb lehet néhány különböző kapcsolatfajtával (erős, alkalmi) modellezni a vizsgált rendszert. Hasonló, bonyolultabb hálózathoz vezet egy olyan rendszer, amelyben különböző aktorokat szeretnénk megkülönböztetni; például a heteroszexuális kapcsolatok hálójában egy él csak férfi és nő között húzódhat.

Tekintsük most mégis azt az egyszerű esetet, hogy egy adott társadalmi kapcsolatrendszer modellezésére egy egyszerű, pontokból és közöttük feszülő egyforma élekből álló hálózatot találtunk megfelelőnek. Nézzük meg, milyen további kérdéseket tudunk ezen a nyelven feltenni. Az egyik leggyakrabban felmerülő kérdés a következő: ha A és B két pontja hálózatunknak, hány, éleken át vezető lépésen keresztül érhetünk el A-ból B-be? Egy buliban például fontos kérdés lehet a következő: „Nem ismersz véletlenül valakit, akin keresztül megismerkedhetnék azzal a jóképű férfival/csinos nővel?” – de egy vállalati kapcsolatrendszerben is nagyon fontos az, hogy ki hány „lépésre” (kézfogásra) van a vezérigazgatótól. A kérdés a konkrét hálózat ismeretében könnyen megválaszolható, és eredményül egy konkrét számot kapunk. Érdekesebb jellemző, hogy mekkora ez a szám átlagosan, azaz A-t és B-t véletlenszerűen választva körülbelül mekkora eredményt kapunk, vagy maximálisan, azaz mekkora a lehető legnagyobb távolság. Nagy, bonyolult hálózatok jellemzésére az előbbi átlagos távolság alkalmasabb, amellyel már megfogalmazhatjuk, hogy mit ért a szaknyelv a „kis világ jelenség” alatt. Egy hálózat „kis világ”, ha az átlagos távolság a hálózatot alkotó pontok (aktorok) számához képest „kicsi”: például ha egy ezer pontot tartalmazó kisvilág-hálózatban az átlagos távolság mondjuk 3, akkor ugyanez a szám egy ugyanúgy szerveződő, egymillió pontot tartalmazó kisvilág-hálózatra csupán 6.

Milgram, amerikai szociológus 1970-es évekbeli kísérletsorozatában különféle csomagokat kellett véletlenszerűen kiválasztott embereknek személyes kapcsolatokon keresztül eljuttatni egy ismeretlen címzetthez. Eredményként azt a következtetést vonta le, hogy az Egyesült Államok több százmilliós lakossága kis világot alkot, hiszen a sikeresen célba ért csomagok átlagosan hat közvetítő kézen mentek keresztül. Nemrégiben Watts és munkatársai hasonló eredményre jutottak email segítségével végzett kísérletükben. Azonban ezeket a következtetéseket több szempontból is óvatosan kell kezelni. Mindkét kísérletben (Wattséknál dokumentáltan) a résztvevők legnagyobb része a társadalom fehér, középosztálybeli részéből került ki, és így e kísérletek semmit sem mondanak hátrányos helyzetű, szegregációban élő emberek csoportjairól. Közelebbről megvizsgálva az eredményeket az is kiderül, hogy az elindított csomagok, illetve email-láncok nagyon nagy része (Wattsék esetében több mint 90%-a) sohasem ért célba, tehát tulajdonképpen azt is mondhatjuk, hogy a kísérletek inkább azt igazolják, hogy a társadalomnak még ez a része is erősen fragmentált, darabjai között nagyon kicsi az átjárás. Nem eldöntött, vajon kis világ-e a társadalom, s még az is elképzelhető, hogy ilyen egyszerű formában nem is eldönthető, azaz különböző módon feltéve a kérdést különböző válaszokat kaphatunk.

A nagyméretű hálózatok egy másik fontos jellemzője a különböző aktorok kapcsolatainak száma és ezen számok eloszlása. Itt azt vizsgáljuk, hogy mekkora annak az esélye, hogy egy adott aktornak 1, 20, 200 vagy akár 1003 kapcsolata legyen. Kiderül, hogy a kapcsolatok számának eloszlása, az ún. fokszám-eloszlás jellemző a különböző hálózatokra és hálózatfajtákra, és ennek tanulmányozásával közelebb kerülhetünk a hálózatot létrehozó folyamatok megértéséhez. Megkülönböztetünk egyenletes eloszlású hálókat, melyekben a fokszámok nem térnek el nagymértékben egy átlagos értéktől, azaz minden aktor nagyjából ugyanannyi kapcsolattal rendelkezik, és szélsőséges fokszám-eloszlású hálókat, melyekben az átlagosnál jóval több, illetve kevesebb kapcsolattal rendelkező aktorokat is szép számmal találunk. Ez utóbbi hálókban természetesen kitüntetett szereppel rendelkeznek a nagyon sok kapcsolattal rendelkező aktorok, akiket divatos szóval huboknak, hálózati központoknak nevezünk.

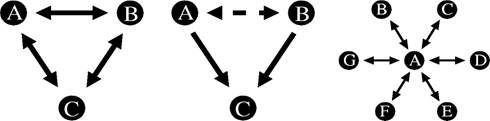
Az átlagos távolság és a fokszám-eloszlás globális jellemzők, melyeket csak akkor tudunk meghatározni, ha az egész hálózatot ismerjük. A szociológiában és a modern hálózatkutatásban egyaránt ismert azonban, hogy a hálók lokális, „helyben tanulmányozható” mintái is fontos információt hordoznak. Az egyik leglényegesebb minta a háromszög vagy triád, amelynek A, B és C aktorai között minden lehetséges élt tartalmaz a hálónk, azaz A ismeri B-t és C-t, akik továbbá ismerik egymást is (1. ábra). Az emberi kapcsolatok hálója tele van háromszögekkel, melyeknek gyakran speciális tartalmuk, jelentésük is van: a „papa-mama-gyerek”, „férj-feleség-házibarát” vagy „főnök-helyettes-beosztott” szerepek mind háromszöghöz vezetnek. A klasszikus „szerelmi háromszög” egy speciális minta: A és B mindketten szerelmesek C-be (két irányított él), s az igazi pikantériát természetesen az jelenti, ha közben A és B jó barátok (1. ábra). Hasonló, többszereplős minta a csillag; ezt akkor kapjuk, ha egy A aktornak sok más aktorral, B-vel, C-vel, D-vel stb. van kapcsolata, akik egymáshoz viszont nem nagyon kapcsolódnak (1. ábra). A központi A aktor gyakran hubnak is tekinthető, azaz sokszor lényegesen több kapcsolata van környezeténél.

A lokális és globális tulajdonságok között félúton találjuk a hálózatok egyik legegyszerűbb, de egyben legtitokzatosabb és talán legnehezebben tanulmányozható aspektusát: a csoportok (clusterek), köznyelven kupacok megjelenését. Emberi kapcsolataink gyakran alakulnak ki társaságokban, ahol egyszerre számos ember teremt egymással kapcsolatot: ilyenek például a munkahelyi, iskolai, sportklubban kötött kapcsolatok. Különböző kupacok között ún. hidak feszülhetnek. Mindennapi életben ilyen híd például két különböző munkahelyen dolgozó ember barátsága. Granovetter, amerikai szociológus figyelte meg azt, hogy ezeknek a hidaknak mennyire fontos szerepük van az információterjedésben még akkor is, ha a híd-kapcsolatok gyakran sokkal gyengébbek, mint az egy közösségen belül feszülők: a közösségben minden belső pletyka hamar elterjed és unalmassá válik, egy kívülről érkező hír azonban sokkal izgalmasabb lehet.

Felmerül a kérdés, hogy egy hosszú idő alatt kialakuló hálóban rekonstruálhatók-e ezek a közösségekre valló kupacok, találunk-e egyáltalán közösségeket? Elképzelhető, hogy a különböző közösségek olyannyira átfedik egymást, hogy egy sűrűn szövött társadalmi hálózatot már egyáltalán nem lehetséges közösségek összességeként felfogni. Bizonyos hálókban azonban, például e-mail és internetes hírcsoport-hálózatokban sikerrel találtak ilyen kupacokat, amelyeket gyakran azonosítani is lehet mint közös érdeklődésű, lakhelyű vagy foglalkozású emberek közösségeit. A csoportok felismerésének problémája közeli kapcsolatban van az alakfelismeréssel, a mesterségesintelligencia-kutatások egyik alapvető kérdéskörével.

Hálózatok modellezése

A modern hálózatkutatás egyik alapvető célja az, hogy feltárja a hálózatok egyszerű, könnyen leírható szabályszerűségeit, és ezek alapján rendszerezze a társadalomban előforduló hálózatokat. A kutatás alapvető módszere a hálózat kialakulásának modellezése: bizonyos egyszerű szabályok felhasználásával generálunk egy mintahálózatot, amelyet összehasonlítunk a megérteni kívánt társadalmi hálózattal. Amennyiben az eredeti és a mintahálózat sok tulajdonsága megegyezik, feltételezhető (bár korántsem bizonyított), hogy az alkalmazott hálózatépítési szabályok valamilyen formában szerepet játszanak a megfigyelt társadalmi háló kialakulásában is.

Az egyik legegyszerűbb kiinduló hálózatmodell a rácsháló (2. ábra), amelyben az aktorok egy rács pontjaiban helyezkednek el, és a kapcsolatok a rács egyenesei mentén feszülnek. Gondolhatunk itt olyan aktorok ismeretségi hálózatára, melyben az aktorok egy négyzetrács, például egy városi utcahálózat rácspontjainál laknak, és mindenki csak a szomszédjaival barátkozik. Könnyen látható, hogy ez a hálózat nem kis világ: miután mindenki csak szomszédjait ismeri, egy nagyméretű „rácsvárosban” az ismeretségi távolságok átlagosan elég „nagyok” lesznek (egy egymilliós „rácsvárosban” több száz összekötőre is szükségünk lehet két kiválasztott pont között). Watts és Strogatz hálózatkutatók mérföldkőnek számító 1998-as cikke ezt a rácshálót vette kiindulópontként, de figyelembe vette azt a lehetőséget is, hogy egy valódi városban az ember eljut szomszédjainál messzebbre is, és „véletlenszerű” kapcsolatot teremt „idegenekkel”. Watts és Strogatz belátták, hogy már egészen kevés „távkapcsolat” is drasztikusan lerövidíti a két tetszőleges aktor közötti szükséges lépésszámot, és ez az egyszerű mechanizmus valóban „kis világgá” változtatja a rácsvárost.

A modellezés egy másik megközelítése abból az egyszerű feltételezésből indul ki, hogy egy szociális hálóban új kapcsolatok az aktorok valamely attribútumával (pl. vagyon, külcsín) arányos valószínűséggel alakulnak ki. Ilyen hálókban spontán módon kialakulnak a sok kapcsolattal rendelkező hubok, a hálók fokszám-eloszlása nem egyenletes. A népszerű Price–Barabási–Albert-modellben az attribútum maga a kapcsolatok száma: népszerű, sok kapcsolattal rendelkező emberek könnyebben kötnek új – bár vélhetően felületes – kapcsolatokat, így valamely mértékben ez a mechanizmus valóban szerepet játszhat a szociális hálók struktúrájának kialakulásában.

A fent már említett közösségek is képezhetik egy hálózatmodell kiindulópontját, melyben az aktorok különböző előre feltételezett kupacokhoz tartoznak, és a kupacokon belül nagyobb eséllyel létesítenek kapcsolatot. E kupacok létrejöhetnek például az ún. szociálisidentitás-vektor figyelembevételével: a társadalom különböző aktoraihoz rendelhetünk identitásukat kifejező értékeket (például vagyoni helyzet, etnikai hovatartozás, nem, iskolázottság stb.). A szociológiában jól ismert jelenség, hogy szociális kapcsolatok nagyobb eséllyel alakulnak ki hasonló identitásvektorral rendelkező aktorok között. Ezek a modellek is kisvilág-hálót hoznak létre, de egy újabb fontos tulajdonsággal is rendelkeznek, amely Watts és Strogatz véletlenszerű távkapcsolatokat tartalmazó modelljére nem teljesül: az aktorok viszonylag könnyen meg is találhatják a rövid utakat egymás között, kizárólag a lokálisan rendelkezésükre álló információk alapján. Egy valódi kis világnak ez is szükséges feltétele: nincs igazán hasznuk a rövid hálótávolságoknak akkor, ha – például egy a Milgraméhoz hasonló kísérletben – ezeket nem tudjuk könnyen megtalálni.

Hálózatok a gazdaságban

A szociális hálók speciális kategóriáját alkotják a gazdasági és kereskedelmi hálózatok, melyekben az aktorok lehetnek emberek, emberek kis közösségei (falvak, települések), de akár nagyvállalatok vagy államok is. Ezek a hálózatok a történelem során párhuzamosan fejlődtek más szociális kapcsolatok hálóival. Előnyük, hogy levelekben, szerződésekben, iratokban gyakran viszonylag jól dokumentáltak, s így rendszerük könnyebben tanulmányozható.

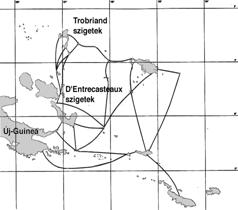
A korai törzsi társadalmak gazdasági kapcsolathálóiról természetesen alig van közvetlen adatunk. A XX. század első felében szociológusok, antropológusok által megfigyelt primitív társadalmak kapcsolatrendszerei azonban feltehetően hasonlítanak ezekre a korai rendszerekre. Ezek közül az egyik legjobban ismert a csendes-óceáni Tobriand-szigetek termékcsere-hálózata, melyet Malinowski, lengyel származású antropológus írt le nagy részletességgel az 1910-es években (3. ábra). Ebben a hálóban a szigetek hozzávetőlegesen egy gyűrű mentén helyezkednek el, és a kapcsolatok szomszédok között feszülnek. Hasonlóan a rácsháló-típushoz, egy ilyen hálózat nem alkot kis világot, hiszen hiányoznak belőle a távoli pontok közötti kapcsolatok. Több más ismert primitív gazdasági háló, például a Pápua-fennsík falvainak kapcsolatrendszere is rácsháló-mintát követ. A közösségek gazdasági kapcsolatait a kölcsönösség (reciprocitás) fogalmával jellemezhetjük: szomszédos közösségek terményeket, kultikus tárgyakat juttatnak el egymáshoz viszonossági alapon, hogy – a kialakult rendszer alapján – később ők maguk is hasonló javakhoz jussanak.

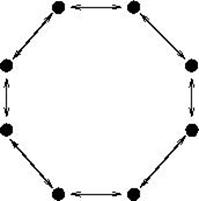
A kölcsönösség mint kapcsolattípus fogalmát Polányi Károly, magyar származású gazdaságtörténész vezette be. Gazdaságelemzésének következő kategóriája az ún. újraelosztási rendszer (redisztribúció), melyet úgy jellemezhetünk, hogy az aktorok egyike kiemelkedik, hierarchikus centrummá válik, és a gazdaság többi szereplője ezen a centrumon keresztül cserél árut. Ennek a hálózatnak a csillagminta adja egyszerű modelljét. Ilyen szerkezetre példa a korai mezopotámiai városállamok templomalapú rendszere, melyben a termény és áru a templombirtokon gyűlt össze, ahol pontos nyilvántartásba került, majd a templomon keresztül jutott el a lakossághoz (4. ábra). A bronzkori Mükéné, a Lineáris B írás kultúrájának gazdasági életében is felfedezhető hasonló szerkezet; ahol a hierarchikus centrum szerepét a királyi palota töltötte be.

Polányi harmadik kategóriája a piacalapú kereskedelem, amelyben önálló aktorok profitszerzés céljából kereskednek. Feltehető, hogy kezdetben ez a fajta kereskedelem is szomszédok között volt csak gyakori, azonban a történelem folyamán a hajózásra és egyéb gyorsan fejlődő közlekedési eszközökre épülő távolsági kereskedelem bonyolult struktúrájú kisvilág-hálóvá fogta össze a kapcsolatrendszer aktorait.

A modern államok kereskedelmi hálózatában (5. ábra) természetesen megjelennek hubok is. Kialakulásukban mindenképpen szerepet játszik a globalizáció, azon belül is, hogy mind több állam gazdasága kapcsolódik be a világkereskedelembe. Az „újonnan érkező” aktorok feltehetően gyakran kapcsolódnak tőkeerős, már korábban is nagyszámú kereskedelmi kapcsolattal rendelkező „régi kereskedőállamokhoz”. Ez pedig nem más, mint a már említett Price–Barabási–Albert-mechanizmus, melynek következtében ezeknek a huboknak a szerepe spontán módon tovább erősödik.

Predikciók és kitekintés

Hogyan is állunk a bevezetőben hangsúlyozott predikciók lehetőségével? Van néhány olyan terület, ahol már most, a szociális hálózatok kutatásának e korai szakaszában is megfogalmazhatunk precíz és hasznos állításokat. Az egyik például az epidemiológia, a fertőző betegségek terjedésének tudománya, amely csak az utóbbi időben kezdett el használni olyan modelleket, amelyek explicit módon figyelembe veszik azt a kapcsolathálót, amelyen a betegségek valójában terjednek. Könnyen belátható, hogy egy kis világot képező hálózaton sokkal gyorsabban terjed el egy fertőzés, mint egy olyan hálózaton, például a rácshálón, amelyben nincsenek hosszú távú kapcsolatok. Ennek fényében különösen érdekes, hogy bizonyos betegségek (például a HIV/AIDS) terjedési görbéje arra utal, hogy a releváns kapcsolatok által kifeszített háló talán nem is kis világ. Egy másik fontos eredmény, hogy ha a kapcsolatok eloszlása elég egyenlőtlen, akkor akármilyen alacsony fertőzékenységű vírus járványt okozhat. Ezzel szemben a klasszikus járványtanban feltételezett kapcsolatrendszerek esetén létezik egy fertőzékenységi határküszöb, amely alatt egy vírus nem képes járványt okozni. Ebből a szempontból tehát alapvető fontosságú, hogy megtudjuk, a vírusterjedés szempontjából jelentős kapcsolati háló tulajdonképpen milyen szerkezetű, hiszen e nélkül a hatékony védekezési mód (oltások, elkülönítés) megválasztása lehetetlen. Egészen másképp kell kezelni egy járványt, ha alapvetően hubokon keresztül terjed, vagy ha a sok háromszög miatt nagyon magas a többszörös fertőzések aránya.

Hasonló megfontolásokat alkalmazhatunk a marketing területén, ahol egy termék vagy fogyasztói szokás elterjedéséről van szó. Meg lehet mérni, hogy bizonyos szokásokra leginkább globális faktorok hatnak (reklám, média stb.), míg mások szociális ismeretségek hálózatain terjednek. Ezen tulajdonságok ismeretében egy-egy konkrét esetben ideális marketingstratégia választható, illetve megállapíthatjuk a terjedés sebességének elvi korlátait.

A marketing kérdésein túlmenően a hálózatkutatás egyik legizgalmasabb és praktikus szempontból is legfontosabb alkalmazási iránya valószínűleg a közgazdaságtanban lesz. A fent említett gazdaságiháló-mintázatok (redisztribúciós csillagok, hubok, rácsok, szerteágazó távoli kapcsolatok) minden bonyolult, modern gazdaságszerkezetben megtalálhatók, és relatív súlyuk, szerepük jellemezhet bizonyos gazdaságstruktúrákat. Ezen a nyelven például pontosan megfogalmazható a posztkommunista országok gazdasági szerkezetének átmenet előtti és utáni különbsége, és osztályozhatók az átmenet típusai. A hálózatoknak gazdaságelméleti kérdésekben is fontos szerepe lehet. A jelenlegi elméleti paradigma központi eleme egy homogén „piac”, amellyel a gazdasági aktorok mint rajtuk kívül álló entitással lépnek kapcsolatba. Valójában persze (és ezt természetesen minden közgazdász tudja) a piac nem egy külső entitás, hanem az összes aktor együttese, és a gazdasági szereplők sem általában a piaccal lépnek kapcsolatba, hanem egymással. Megfelelő adatok birtokában kísérletet lehet tenni arra, hogy a gazdasági modelleket az aktorok közötti explicit hálózaton értelmezzük. Ebben az esetben például az úgynevezett piaci hatékonyság, illetve annak hiánya a hálózat struktúrájából következhetne, hiszen egy adott szereplő csak azokkal tud kapcsolatba lépni, akik a hálózatban számára elérhetőek.

A szociális hálók kutatása, a különböző mintázatok, modellek összehasonlítása, a terjedési jelenségek és egyéb dinamikus folyamatok tanulmányozása feltehetően sok újdonságot tartogat még számunkra, melyek közelebb visznek a szociális hálózat egészének modellezéséhez, a társadalom és a gazdaság pontosabb megértéséhez. A továbblépés egyik legfontosabb akadálya jelenleg az adathiány: vizsgálataink explicit hálózati modelleket használnak, s a modellek pontossága, a következtetések ellenőrzése csak pontosan dokumentált hálókon lehetséges. A legfontosabb feladat ezért a legkülönfélébb szociális hálózatok szisztematikus feltárása, amelyhez szociológusok, járványkutatók, gazdaságkutatók, etológusok, médiakutatók mind hozzájárulhatnak a maguk területén.

            1. ábra Egyszerű hálózati minták: háromszög, „szerelmi háromszög” és csillag

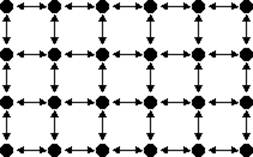2. ábra Rácsháló

3. ábra Kölcsönösségi rendszer: A Pápua Új-Guineától keletre eső Tobriand-szigetek Kula-kereskedelme Malinowski után; modellje: a rácshálóhoz hasonló gyűrűháló

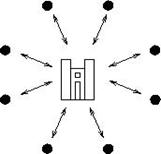4. ábra Újraelosztási rendszer: árucsere a templomgazdasággal, azaz a csillagháló

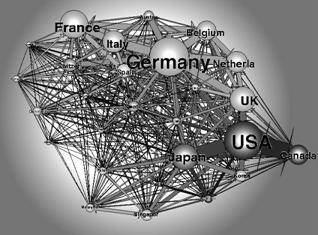5. ábra Piac: a világ államainak sűrű kereskedelmi hálója