Válóperes tárgyaláson vagyunk. A férj beismeri, hogy megcsalta a feleségét. „Nem volt más választásom”, mondja. „Nem lettem volna képes elviselni azt a megaláztatást, hogy a feleségem esetleg felszarvaz, miközben én hű maradok hozzá.” „Honnan vette, hogy a felesége megcsalja?”, kérdezi a bíró. „Nem tudtam, csak gondoltam. Úgy okoskodtam, hogy ha nem csal meg, akkor is jobban járok a félrelépéssel, mivel az új és kellemes élményeket jelent számomra. Ráadásul ebben az esetben én vagyok a győztes.” „És Ön, Asszonyom?”, szól a bíró. „Én pontosan ugyanezt tudom elmondani”, vallja be elpirulva a feleség.
Kétszereplős játékok
A fiatal Neumann János egyik nagyszerű ötlete alapján 1928-ban létrehozta a játékelméletet [Neumann]. Eredetileg hétköznapi kétszereplős helyzetek tanulmányozására szolgált, ahol mindegyik résztvevőnek olyan döntéseket kell hoznia, hogy az eredmény a lehető legelőnyösebb legyen számára, ami persze nemcsak a saját döntésétől, hanem az ellenfeléétől is függ.
Nagyon hamar kiderült, hogy ez az elmélet nemcsak a kétszereplős szórakoztató játékok elemzésére alkalmas, hanem igen sok gyakorlati alkalmazása is van. Erre elsőnek a közgazdászok jöttek rá, hiszen a piac is tulajdonképpen egy játék [Neumann–Morgenstern].
Neumann munkája először csak kétszereplős, állandó összegű játékokra vonatkozott. (A pontozás módjától függően a játék összege lehet bármilyen állandó. Ez azonban csak a skála eltolását jelenti, ezért az állandó összegű játékokat gyakran nullaösszegűeknek is nevezik.) Ilyen például a sakk, hiszen az egyik játékos nyeresége a másik vesztesége. Ezt tiszta konfliktusnak nevezzük.
Neumann feltételezte továbbá, hogy a szereplők mindig a lehető legjobb lépést választják (racionalitás), és ismerik a saját maguk és az ellenfél által hozott különböző döntések összes lehetséges kimenetelét (teljes információ). Az ilyen játékokra optimális stratégiákat dolgozott ki, amelyekkel mindkét játékos a lehető legjobb eredményt érheti el. Neumann ún. minimax-stratégiája alapján lehet például olyan számítógépes programokat írni, amelyek szinte mindenkit megvernek, például az Otello (Reversi) játékban, mivel a számítógép egyetlen lépést sem néz el, ellentétben velünk, gyarló emberekkel.
A legegyszerűbb kétszereplős játékok esetén mindkét résztvevőnek mindössze két választási lehetősége van. Jelöljük ezeket C-vel és D-vel. Ennek megfelelően négy különböző eredmény képzelhető el: CC, CD, DC és DD (az első választás az első játékosra, a második a másodikra vonatkozik). A játék lehetséges kimeneteleit a következő táblázat szemlélteti:
C D
C a1, a2 b1, b2
D c1, c2 d1, d2
1. táblázat
Az első játékos választhat a sorok, a második az oszlopok között. Attól függően, hogy mit választottak, mindketten különböző jutalmakat (büntetéseket) kapnak. Ha például az első játékos C-t, a második D-t választ, akkor az első jutalma b1, a másodiké b2 lesz. Kizárjuk továbbá azt a lehetőséget, hogy valamelyikük is egyforma jutalmat kap különböző kimenetelek esetén. Mivel a1, b1, c1 és d1 éppúgy, mint a2, b2, c2 és d2 külön-külön 4 x 3 x 2 x 1 = 24-féleképpen helyezhető sorrendbe, ezért láthatjuk, hogy még ebben a nagyon egyszerű esetben is 24 x 24 = 576 különböző játék képzelhető el. A helyzetet némileg egyszerűsíti, hogy a sorok, illetve oszlopok, valamint a játékosok felcserélésével gyakorlatilag azonos játékokhoz jutunk. Ha ezeket elhagyjuk, az eredmény még mindig 78 különböző játék [Rapoport–Guyer]. A 78 különböző eset között csak három állandó összegű játékot találunk.
Tekintsünk egy példát a fenti táblázatra:
C D
C 3, 3 1, 4
D 4, 1 2, 2
2. táblázat
A számok itt csupán a jutalmak nagyságának sorrendjét és nem a jutalmak nagyságát jelölik, vagyis azt jelentik, hogy ebben az esetben c1 > a1 > d1 > b1 és b2 > a2 > d2 > c2.
Könnyű észrevenni, hogy ez egy szimmetrikus játék (a1 = a2, b1 = c2, c1 = b2 és d1 = d2), mivel a két játékos felcserélésével ugyanazt a jutalomtáblázatot kapjuk. A 78 különböző játék közül 12 szimmetrikus.
Ezt a játékot 1950-ben a Rand Corporation kutatói találták ki az egyéni és a kollektív racionalitás közötti kibékíthetetlen ellentmondás, vagyis az emberi társadalom tökéletlenségének szemléltetésére. Fogolydilemmának nevezték el, mert az eredeti megfogalmazásban két bűnözőről volt szó. Ha bármelyikük vallomást tesz a másikra, miközben az hallgat, akkor az első szabadlábra kerül, míg társa életfogytig ülhet a börtönben. Legjobban akkor járnának, ha mindketten hallgatnának, mert akkor nem lenne döntő bizonyíték ellenük, és viszonylag kis büntetést kapnának. Igen ám, de mindketten szabadulni akarnak, ezért el fogják árulni egymást, és ennek következtében együtt ülhetnek hosszú ideig. Vagyis mindegyikük számára a rossz döntés tűnik előnyösnek.
Szinte nincs a társadalmi életnek egyetlen olyan területe sem, ahol a fogolydilemma ne jelentkeznék. Irodalma hatalmas. Már 1965-ben komoly monográfia jelent meg róla [Rapoport–Chammah]. A nyolcvanas években versenyt hirdettek számítógépes programok között, melyeknek ismételt fogolydilemma-játékokat kellett egymással játszaniuk a bajnoki címért, ami a legnagyobb pontszámot elérő programnak jutott [Axelrod]. Az ismételt játék abban különbözik az egylépésestől, hogy itt mód nyílik az ellenfél előző lépéseit az ismételt játék során figyelembe venni és azokra reagálni. A verseny nyomán világossá vált, hogy sikert csak akkor érhetünk el, ha eltérünk a racionalitástól. A versenyek iránti nagy érdeklődést mutatja, hogy az eredményesnél eredményesebb kétszemélyes dilemma-algoritmusok még ma is egymást követik [Hoffmann].
A 2. táblázat segítségével könnyen bevezethetünk néhány fontos játékelméleti fogalmat. Mivel 4 > 3 és 2 > 1, mindkét játékos számára mindig D előnyös, függetlenül a másik játékos választásától. D tehát domináns stratégia mindkét játékos számára, és ennek következtében DD az egyensúlyi helyzet, amit legtöbbször Nash-egyensúlynak neveznek. (Névadójáról szól az Egy csodálatos elme című film.) Ha bármelyik játékos egyedül hagyja el az egyensúlyi helyzetet, rosszabb helyzetbe kerül. Ezt láttuk a bevezető szituációban is: mindkét „játékos” a félrelépést (D) választotta, mert – házastársa cselekedetétől függetlenül – ez volt számára előnyösebb.
Azt is látjuk viszont, hogy mindkét játékos akkor járna legjobban, ha hűek maradnának egymáshoz (CC). Ezt Pareto-optimális helyzetnek nevezzük (Vilfredo Pareto olasz közgazdász után.) Az egyensúly (DD) ebben az esetben fogyatékos, mivel a válás távolról sem a legjobb megoldás.
Könnyen belátható, hogy ha bármelyik játékos rendelkezik domináns stratégiával, akkor a játéknak egy egyensúlyi helyzete van, ha azonban ez egyiknek sincs, akkor vagy két egyensúly van, vagy egy sincs.
Dilemmák
A sokszereplős játékok szempontjából elsősorban a szimmetrikus játékok lesznek érdekesek, ezért ezen játékok tárgyalásának megkönnyítésére általánosítsuk a 2. táblázatot:
C D
C R, R S, T
D T, S P, P
3. táblázat
Amint láttuk, a fogolydilemma esetében T > R > P > S. Ha az irodalomban elterjedt angol szavaknak megfelelő jelöléseknek értelmet adunk, megértjük a dilemma mélységét. C az együttműködést (cooperation), D a hűtlenséget (defection) jelenti. Ha mindkét játékos hajlandó együttműködni, R jutalmat (reward) kapnak, ha mindketten megpróbálják becsapni egymást, P a büntetésük (punishment). Ha az egyik játékos hűtlen, miközben a másik kooperálna, a hűtlen bedől a nagy T kísértésnek (temptation), a pórul járt együttműködő viszont nagy S árat (sucker’s payoff) fizet balekságáért.
A fogolydilemma nem az egyetlen társadalmi dilemma. Az irodalomban nem alakult ki a dilemmák egységes definíciója. Véleményem szerint dilemmák azok a szituációk, amikor a kísértés a hűtlenségre nagyobb, mint a közös jutalom, és ez nagyobb, mint a közös büntetés (T > R > P). Ilyenkor érdemes megpróbálni a hűtlenkedést, bár a közös együttműködés előnyösebb, mint a közös hűtlenség. A szimmetrikus játékok között négy dilemmát találunk – minden esetben feltételezzük, hogy a játékosok nem ismerik társuk döntését:
Fogolydilemma (T >R > P > S). Egyensúly: DD (lásd fent).
Gyávanyúl-dilemma (T > R > S > P). Ez a vad tinédzserek játéka volt az ötvenes években, amit egy amerikai filmben is megörökítettek. Lényege egy olyan autóverseny, amikor a két játékos autóval egymás felé száguld. Aki kitér (azaz együttműködni próbál), azt gyáva nyúlnak csúfolják, míg a másikat (a hűtlenkedőt) hősként ünneplik. A tét nem kevés. Hiszen ha mindketten kitérnek (CC), akkor ugyan mindketten életben maradnak, de egyikük sem lesz hős. Ezzel szemben ha egyikük sem tér ki (DD), akkor mindketten belehalnak a hősködésbe. A T > R > S > P egyenlőtlenségek teljesülése esetén a 3. táblázat segítségével látható, hogy CD és DC az egyensúlyi helyzetek. Ennek a dilemmának tipikus példája a hidegháború. A két szuperhatalom állandóan fenyegette egymást, ám végül is egyikük mindig engedett, hogy ne következzék be nukleáris katasztrófa.
A gyávanyúl-dilemma jóindulatú változata (T > S > R > P). Továbbra is CD és DC az egyensúlyok és DD a legrosszabb megoldás. A gyáva nyúl azonban most jobb helyzetben van, mint az előző esetben, hiszen bölcs döntéséért nagyobb jutalmat kap, mintha mindketten kitértek volna.
Vezérdilemma (S > T > R > P). A régi vicc szerint két japán közül az az udvariasabb, aki kevésbé udvarias, mert megengedi, hogy a másik legyen az udvariasabb. Képzeljük el, hogy a két japán egy szűk ajtón akar keresztülmenni. Ellentétben a gyáva nyúllal, az együttműködő most a vezér szerepét játssza, aki vállalja a kevésbé udvarias szerepét, és elsőnek indul el. Ő kapja az önzetlen japánnak kijáró legnagyobb jutalmat. A vezér cselekedete azonban a hűtlen számára sem előnytelen, hiszen míg a vezér jut át először az ajtón, az udvariasabb szerepében tetszeleghet. Baj csak akkor van, ha mindketten ugyanazt teszik. Ha mindkettő vezér akar lenni (CC), akkor csak egymáshoz préselődve jutnak át az ajtón, ha viszont egyik sem (DD), akkor örökké az ajtó előtt fognak hajlongani. Az egyensúlyok ismét CD és DC esetében lépnek fel.
Az irodalomban érdeklődés mutatkozott több más játék iránt is, mivel – bár a fenti definíciónak nem felelnek meg – ezek sem vezetnek egyértelmű stratégiához, így hétköznapi értelemben ezek is „dilemmák”. Lássunk közülük hármat:
Nemek harca (T > S > P > R). Egy házaspár mindkét tagja szeretné az estét a párjával együtt tölteni, de jól tudják, hogy a férj futballmeccsre menne szívesebben, a feleség pedig színházba. Az együttműködő hajlandó engedni a másik kívánságának, a hűtlen viszont ragaszkodik a sajátjához. Legjobban az a fél jár, aki nem enged, míg a párja engedékeny. Aki enged, valamivel rosszabbul jár, mert nem a kívánsága szerint tölti az estét, de legalább együtt lehetnek. Mivel nem ismerik egymás döntését, ezért ha mindketten engednek (CC), vagy egyikük sem (DD), akkor nem lehetnek együtt, de CC még rosszabb, mint DD, mivel CC esetén egyikük sem azt csinálja, amit szeretne. Egyensúlyok: CD és DC.
Szarvasvadászat (R > T > P > S). Ezt a játékot Jean Jacques Rousseau találta ki a társadalmi érdek szemléltetésére. Két vadásznak arra a kérdésre kell válaszolnia, hogy szarvasra (C) vagy nyúlra (D) akar-e vadászni. Akkor járnak legjobban, ha mindketten a szarvast választják. Ha azonban csak egyikük dönt a szarvas mellett, akkor hoppon marad, mert egyedül nem sokra megy, míg a társa lő egy nyulat, és ráadásul övé a siker öröme is. Ha egyikük sem akar együttműködni, mindkettőnek meg kell elégednie egy-egy nyúllal. Egyensúlyok: CC és DD.
Holtpont (T > P > R > S). Ebben a játékban mindkét versengő a másiktól várja, hogy engedjen, de azt egyikük sem teszi, mivel – a fogolydilemmához hasonlóan – mindkettőnek a hűtlenség a domináns stratégiája, ezért az egyensúly itt is DD-nél alakul ki. Ebben az esetben azonban a kölcsönös hűtlenség egyben a Pareto-optimális helyzet is, ezért a Holtpont végképp nem tekinthető dilemmának.
Láthatjuk, hogy a játékoknál a lényeg a jutalmak viszonya egymáshoz, illetve azok számszerű értéke.
Sokszereplős játékok
Az élet által létrehozott valóságos „játékoknak” rendszerint több mint két szereplője van, sok esetben akár több millió is. Ezek távolról sem állandó összegűek, hiszen gyakran előfordul, hogy minden résztvevő veszít (pl. racionális fogolydilemma), vagy éppen nyer (becsületes szabadpiac). Teljes információ szinte sohasem áll rendelkezésre (amikor beülök az autómba, még fogalmam sincs arról, hogy egy váratlan baleset következtében mekkora forgalmi dugó lesz az autópályán). A racionalitás feltételezése egyenesen naiv, hiszen az embereket döntéseiknél nem éppen az ésszerűség vezeti.
A gyakorlatban alkalmazható játékelméletnek tehát sokszereplős, nem racionális, nem állandó összegű, nem teljes információjú játékokat kell tárgyalnia.
Mielőtt rátérünk arra, hogy mindez miként lehetséges, és mi mindent kell figyelembe venni ezen sokszereplős játékok modellezéséhez, megemlítek egy fontos különbséget a kétszereplős és a sokszereplős játék között. A kétszereplős játék befejezése után pontosan lehet tudni, hogy melyik játékos mit lépett, míg sokszereplős játék esetén a felelősség megállapíthatatlan. A hűtlen viselkedés által okozott kár megoszlik az összes résztvevő között. Pontosabban: a jutalmak és büntetések mértékét az együttműködők aránya, vagyis a játékosok döntésének statisztikus eloszlása határozza meg.
Mint említettem, a fogolydilemma számtalan társadalmi jelenségre jellemző. Példa erre a legelő tragédiája [Hardin], amelyet a későbbiekben részletesen fogunk elemezni. Angliában még ma is szokásban van, hogy kisebb falvak közös legelőt tartanak fenn a lakosok állatainak ellátására. Képzeljük el, hogy egy faluban száz család él, és mindegyiknek egy tehene van. A legelő éppen ennyi tehén számára nyújt elegendő táplálékot. Miután beköltöztem a faluba, észreveszem, hogy elfér még egy tehén a legelőn, veszek tehát még egy jól tejelő tehenet, kihajtom a legelőre, és a felesleges tejet eladom a piacon, miáltal többletjövedelemhez jutok (hűtlen viselkedésem jutalma). A baj akkor kezdődik, amikor a szomszédaim sem akarnak lemaradni, és hamarosan kétszáz tehén próbál megélni a legelőn. Ez az adott körülmények között lehetetlen. Valamennyi állat elpusztul, természetesen az enyémek is, így bosszulva meg hűtlenségemet.
Az emberek azonban szerencsére nem mind ilyenek, különböző módon reagálnak felelőtlen viselkedésemre. Az együttműködők aránya a résztvevők személyiségétől és vérmérsékletétől függ. Ennek következtében olyan egyensúlyi helyzet jön létre, amely merőben különbözik a totális katasztrófától. Vannak olyan emberek, akik annyira jóindulatúak, hogy még akkor sem vesznek még egy tehenet, ha már legtöbb szomszédjuk ezt tette. Mások csak a szomszédjaik viselkedését figyelik, és figyelmen kívül hagyják a falu többi lakosát. Sokan csak cselekedeteik közvetlen következményével számolnak, megint mások pontosan megfigyelik korábbi viselkedésük hatását is, és így tovább. A résztvevők személyisége tehát meghatározó jelentőségű.
Kicsoda-micsoda
A játékelmélet kezelni tudja a sokszereplős játékokat, amelyek igen bonyolultak, és számuk végtelen. A játékok elemzéséhez mindenképpen tisztáznunk kell a következő kérdéseket [Szilagyi 3]:
1) Kik a játékosok? Lehetnek személyek, csoportok, szervezetek, népek, államok, idegsejtek, rovarok, számítógépek stb. A szakirodalomban ezeket ágenseknek nevezzük. Az ágensek olyan egységek, amelyek képesek a környezet hatásaira önálló döntésekkel válaszolni. Lehetnek nagyon egyszerűek vagy igen bonyolultak, de közös tulajdonságuk, hogy egymással kölcsönhatásban állnak. Például az agy nem egyszerűen több milliárd idegsejt összessége, hanem az idegsejtek állandóan változó kölcsönhatásai révén működő szerv.
2) Milyen döntési lehetőségek között választhatnak? Minden döntési szituáció bizonyos lehetőségekre korlátozódik. Egyszerű esetekben két lehetőség közül kell választani (kihajtok-e még egy tehenet a legelőre), de az élet ennél sokkal bonyolultabb helyzeteket is produkál (például mekkora öszszeggel járulok hozzá egy önkéntes közös alaphoz).
3) Milyen információ áll rendelkezésükre? A résztvevők ismerik-e partnereik döntéseit? Teljes információ csak akkor áll rendelkezésre, ha a játékosok ismerik a saját maguk és minden partnerük által hozott különböző döntések összes lehetséges kimenetelét. Ez a legtöbb esetben lehetetlen. Mielőtt útra kelünk, csak részben támaszkodhatunk az utak helyzetére vonatkozó közlekedési hírekre.
4) Tárgyalhatnak-e egymással játék közben? Létrehozhatnak-e koalíciókat? Ez a politikai és közgazdasági játékelmélet alapkérdése. Természetesen erre csak akkor van lehetőség, ha a játékosok ismerik a partnereiket (az előző példában nem ismerik). Még ha ismerik is egymást, nem biztos, hogy képesek kommunikálni. A koalíciók azonban alapvetően megváltoztathatják a játék képét. Gondoljunk csak a politikai pártok közötti alkudozásokra!
5) A játékosok lépései egyszerre történnek vagy időben el vannak osztva? Ez is nagy különbség. Az első esetben minden játékos ugyanazt a környezetet tapasztalja, amikor döntését meghozza. A legtöbb valóságos esetben azonban a különböző ágensek különböző és egymással összefüggésben nem levő időpontokban hozzák meg döntéseiket. Ennek következtében mindegyikük egy kissé különböző világot érzékel maga körül, mint a többiek. Az ilyen helyzeteket nehezen tudja kezelni a játékelmélet.
6) Mi a játék célja? A racionális játékosok a lehető legnagyobb jutalmat próbálják megszerezni maguknak. A számítógépes programok közötti verseny esetén – amelyről korábban beszéltünk – a cél a legnagyobb pontszám elérése volt. Egyes játékosok akkor boldogok, ha többre jutnak, mint a szomszédaik, mások viszont nem kívánnak kitűnni társaik közül.
A valóságban a különböző játékosok céljai nem mindig azonosak. Az is előfordulhat, hogy nincs különösebb céljuk, hanem csupán reagálnak a külvilágtól kapott impulzusokra (például az idegsejtek). Gyakorlati szempontból nem az egyének boldogulása érdekes, hanem az, hogy mi a játék társadalmi eredménye bizonyos adott feltételek teljesülése esetén.
7) Hány lépésből áll a játék? Az egylépéses játékok tanulmányozása nem különösen érdekes. A valódi játékok általában ismétlődnek (minden nap újra el kell döntenem, hogy autóval indulok-e el hazulról).
8) Többlépéses játék esetén hogyan határozzák meg a következő lépést? Az újabb döntések a játékosok személyiségétől, saját és szomszédaik előző döntéseitől, valamint a környezettől kapott jutalmaktól/büntetésektől függnek. A játék elemzéséhez pontosan tudnunk kell, hogy ezek a tényezők milyen módon hatnak a következő döntésre.
9) Mikor tekintjük a játékot befejezettnek? Az ismétlődő játékot akkor tekintjük befejezettnek, ha valamely fontos paramétere (például az együttműködők aránya) egy bizonyos helyzethez tart vagy akörül ingadozik. Ezt a helyzetet nevezzük a játék eredményének.
10) Milyenek a játékosok alapvető tulajdonságai? Ennek a kérdésnek meghatározó szerepe van a játékok tanulmányozásában. Az ágensek általában nagyon bonyolultak. Gondoljunk csak az idegsejtre, amelynek közelítő matematikai leírását Nobel-díjjal jutalmazták [McCulloch–Pitts]. Egy ideghálózat leírásához azonban elég, ha annyit tudunk, hogy mikor van egy idegsejt aktív állapotban.
Ugyanez a helyzet az emberekkel is. Minden ember egy külön világ, de a társadalom szempontjából elegendő a legfontosabb tulajdonságaikat ismerni. Az emberi személyiség leírására sokféle módszert használnak a pszichológusok. Ezek közül legfrappánsabbnak azt az ötletet tartom, miszerint valamennyien 14 alapvető elmekórtani rendellenesség kombinációi vagyunk [Oldham–Morris]. Baj csak akkor van, ha valakiben e rendellenességek egyike vagy másika elnyomja a többit. Eszerint minden embert 14 számmal lehet jellemezni, ami elég kényelmes megoldásnak tűnik, bár ezt a módszert ma még senki sem alkalmazza a játékelméletben.
A játékok leírásánál további egyszerűsítéssel élünk. Azt feltételezzük, hogy az ember az önzés, a konformizmus, a feltételes reflexek és némi kis racionalitás keveréke. Aszerint, hogy melyik tulajdonság jellemző ránk elsősorban, különbözőképpen reagálunk a külvilágtól kapott ingerekre. Vagyis az irodalomban általában feltételezett egyformaság semmiképpen sem fogadható el.
11) Változik-e a személyiségük a játék során? Előfordul, hogy élettapasztalata alapján valaki annyira megváltozik, hogy más személyiségkategóriába kerül. Ez lehetséges egy sokszor ismétlődő játék során is, ha képesek vagyunk addigi kudarcainkból levonni a szükséges következtetéseket.
12) Megtagadhatja-e valamelyik játékos a játékban való részvételt? Sakkozni nem lehet úgy, hogy az egyik játékos átengedi a másiknak az őt megillető lépést. Kutuzov azonban úgy verte meg Napóleont, hogy lehetőleg kitért a csaták elől. A részvétel megtagadása tehát nagyon is valóságos lehetőség.
13) Milyenek a jutalom/büntetés-függvények? Ha minden más paramétert rögzítünk, akkor a jutalom/büntetés függvények határozzák meg a játék kimenetelét, ahol az együttműködők arányát tekintjük független változónak. A függvények egymáshoz képest elfoglalt helyzete legtöbbször nem elegendő a játék leírásához, a jutalmak és büntetések számszerű értékeit is ismernünk kell. A gyakorlati alkalmazások szempontjából a legnehezebb feladat a jutalom/büntetés-függvények pontos meghatározása valóságos adatok alapján.
14) Szimmetrikus-e a játék? A játék akkor szimmetrikus, ha minden játékos jutalom/büntetés-függvényei azonosak.
15) Hogyan viszonyul a játékosok összegzett jutalma a kívánatos döntést hozók arányához? Az egész társadalom teljes jutalma nem mindig akkor a legnagyobb, amikor a legtöbben hoznak kívánatos döntést. Ennek következtében nem mindig előnyös a résztvevőket „jó viselkedésre” kényszeríteni. Gondoljunk arra, hogy az állam milyen komoly bevételektől esne el, ha senki sem sértené meg a közlekedési szabályokat.
16) Hol helyezkednek el a játékosok? A játékosok térbeli elhelyezkedése sokféleképpen történhet. Az is előfordulhat, hogy több játékos foglalja el ugyanazt a területet.
17) Képesek-e mozogni? A fent említett esetben, vagy ha kevesebb játékos van, mint amennyi hely rendelkezésükre áll, a játékosok mozoghatnak is. Bonyolult társadalmi helyzetek leírásához ezt figyelembe kell vennünk [Epstein–Axtell]. Ebben az esetben a résztvevők szomszédsága állandóan változik.
18) Milyen messzire terjed a kölcsönhatás közöttük? A társadalom tagjai többnyire csak szűk környezetükkel vannak közvetlen kapcsolatban. A teljes társadalommal azért alakul ki kapcsolatuk, mert környezetük környezete más elemeket is tartalmaz. Az ágenseket tehát sejtautomatáknak tekinthetjük, amelyek viselkedését saját és szomszédjaik állapota határozza meg egyszerű szabályok alapján. Már a legegyszerűbb ilyen szabályok is rendkívül bonyolult struktúrákat képesek létrehozni [Gardner]. A sejtautomaták tanulmányozása annyira érdekes, hogy megérdemelne egy különálló dolgozatot. Egyesek szerint a tudomány szinte minden problémáját rajtuk keresztül lehet megközelíteni [Wolfram].
19) Hogyan határozzuk meg a kölcsönhatás mélységét? Pontosan meg kell határoznunk, hogy mit értünk környezeten. Legegyszerűbb a közvetlen szomszédokra korlátozódó környezet. A távolabb elhelyezkedő ágensek kisebb-nagyobb mértékben szintén befolyásolhatják a szóban forgó ágens viselkedését. Az is előfordulhat, hogy mindenki mindenkivel közvetlen kapcsolatban áll. Ebben az esetben a résztvevők összessége a környezet. A kölcsönhatás mélysége az a legnagyobb távolság, amilyen távol elhelyezkedő ágens még az előző ágens környezetéhez tartozónak tekinthető.
Természetesen ennyi paraméter esetén nagyon nehéz még a játékok rendszerbe foglalása is, vizsgálatukról nem is beszélve. Ha valamennyi többi paramétert rögzítjük is, még mindig végtelen sok játék marad, mivel a lehetséges jutalom/büntetés-függvények száma végtelen. Mindezek a játékok az életben előforduló végtelen számú szituáció egyikét reprezentálhatják.
Szerencsére Neumann János olyan eszközt is adott nekünk, amely lehetővé teszi az igen bonyolult játékok tanulmányozását is. Ráadásul a ma rendelkezésre álló számítógépek segítségével sokszereplős játékok komoly elemzését is elvégezhetjük, sőt ezeket alkalmazhatjuk is társadalmi jelenségek vizsgálatára.
A modell
A sokszereplős játékok szimulációjához először is meg kell határoznunk, hogy mit akarunk modellezni, vagyis választ kell adnunk a fenti kérdésekre.
Az itt szereplő egyszerű modell nem korlátozódik személyekre, hanem bármilyen ágensek esetén érvényes, akik két lehetőség közül választhatnak. Jelöljük ezeket a fentiekhez hasonlóan C-vel és D-vel. Az egyetlen információ, amely rendelkezésükre áll, a környezettől kapott jutalom vagy büntetés. Játszótársaikról semmit sem tudnak, ennek következtében alkudozni sem képesek velük, és nem alkothatnak koalíciókat. A játékosok lépései egyszerre történnek.
A játékosokat stochasztikus sejtautomatáknak tekintjük. Ez azt jelenti, hogy a játék kezdetén a sejtautomata bizonyos p valószínűséggel választja az együttműködést. Ez a valószínűség nem a sok szereplő következménye, hanem minden egyes automata alapvető tulajdonsága. A valószínűség a szomszédok viselkedésétől függően, valamint a játék során kapott jutalmak/büntetések hatására állandóan változik. A szomszédok cselekedetei tehát nem egyértelműen határozzák meg az automata döntését, csak annak valószínűségére vannak hatással. Jutalom esetén az előző választás megismétlésének valószínűsége növekszik, büntetés esetén csökken.
A játék célja egyszerű társadalmi jelenségek vizsgálata adott feltételek teljesülése esetén. Ismétlődő játékot vizsgálunk, amelyet akkor tekintünk befejezettnek, amikor az együttműködők aránya egy bizonyos értéken stabilizálódik vagy akörül ingadozik. A játékosok lépései az előző lépésekért kapott jutalomtól/büntetéstől, személyiségüktől, valamint az együttműködők mindenkori arányától függnek.
A játékosok személyiségeinek a következő, könnyen modellezhető tulajdonságokat, valamint ezek tetszés szerinti kombinációit feleltetjük meg [Szilagyi 2]:
Pavlovi: a p valószínűség a környezettől kapott jutalom vagy büntetés arányában növekszik vagy csökken. A Pavlov által vizsgált feltételes reflexeknek megfelelően azokat a cselekedeteket szokjuk meg, amelyek számunkra kedvező körülményekhez vezetnek.
Könyvelő: az előző döntések nyomán kapott jutalmakat/büntetéseket nyilvántartja, és az új döntésre vonatkozó valószínűség ezek átlagától függ.
Konformista: szomszédjai többségének döntéseit követi.
Mohó: annak a szomszédnak a döntését utánozza, aki a legnagyobb jutalmat kapta.
Eltökélt: nem törődik a jutalmakkal/büntetésekkel. A p valószínűség állandó. Ennek speciális esetei:
Rosszindulatú: mindig hűtlen (p = 0).
Kiszámíthatatlan: teljesen véletlenszerűen cselekszik (p = 0,5).
Jóindulatú: mindig együttműködik (p = 1).
A szimuláció során az ágensek tulajdonságai nem változnak, de egymástól különbözhetnek, és a szereplők a játékban való részvételt nem tagadhatják meg.
A jutalom/büntetés-görbéket tetszés szerinti függvények határozhatják meg, ezáltal nagyon sok különböző társadalmi jelenség vizsgálata válik lehetővé. Feltételezzük, hogy a vizsgált játékok szimmetrikusak, vagyis minden játékos jutalom/büntetés-függvényei azonosak.
A játékosok egy síkban helyezkednek el. Számukat – ami akár több millió is lehet – csak a számítógép virtuális memóriája és a képernyő felbontóképessége korlátozza. A játékosok az itt tárgyalt esetekben nem mozoghatnak. A sejtautomaták közötti kölcsönhatások mélységét tetszés szerint állíthatjuk be.
Eredmények
Az előbbiekben leírt modell alapján számítógépes programokat írhatunk, amelyek az adott körülményeknek megfelelő társadalmi jelenségeket szemléltetik. A szimuláció során az együttműködők aránya folytonosan változik, mivel az ágensek választására vonatkozó valószínűségei szüntelenül változnak a jutalom/büntetés-függvények értékei arányában. E változások a többi ágens döntéseitől, valamint az ágensek személyiségétől is függnek. A számítógép képernyőjén minden újabb lépés után megjelennek az éppen C-t és D-t választó ágensek, állapotuknak megfelelő színezéssel. Az itt következő ábrákon a fekete ágensek éppen C-t, a fehérek D-t választottak. A játékot az idő függvényében grafikusan is követhetjük. Minden ágens állapotára vonatkozóan külön-külön is felvilágosítást kaphatunk [Szilagyi–Szilagyi 1].
Nézzünk néhány konkrét példát olyan társadalmi jelenségekre, amelyeket a tárgyalt modell segítségével elemezhetünk; ezek közül az elsővel részletesebben foglalkozunk, a többinél felvillantunk néhány érdekességet [Szilagyi 1].
A legelő tragédiája
Az együttműködők, illetve a hűtlenek C(x), illetve D(x) jutalom/büntetés-függvényeit egy speciális esetben az 1. ábrán láthatjuk. Ha az együttműködők arányát x-szel jelöljük, akkor az ábrán látható függvényeket a D(x) = 2x – 0,5, illetve a C(x) = 2x – 1 egyszerű lineáris összefüggések írják le. Ha majdnem mindenki együttműködik, mindenki jutalmat kap, különösen azok a kevesek, akik a hűtlenséget választják. Ezek jutalma mindig nagyobb, mint az együttműködőké, de ha már túl sokan vannak, akkor mindenki büntetést kap (kipusztulnak a tehenek). Ez tehát a fogolydilemma sokszereplős általánosítása. Erről könnyen meggyőződhetünk, ha a P, R, S és T értékeket elhelyezzük a megfelelő függvények kezdetén és végén. Láthatjuk, hogy T > R > P > S valóban.
Feltételezzük, hogy a résztvevők valamennyien a pavlovi kategóriába tartoznak, és mindenki mindenkivel kölcsönhatásban van. A szimuláció egy bizonyos kezdeti állapotból indul, ami az együttműködők kezdeti arányának felel meg (2. ábra). Ez az arány kb. 100 lépésig állandóan változik (3. ábra). Az együttműködők átlagos jutalma xC(x), a hűtleneké pedig (1 – x) D(x). Egyensúlyi helyzet akkor alakul ki, ha e két érték azonos [Szilagyi–Szilagyi 2]. Ennek az egyensúlyi egyenletnek legtöbbször két valós megoldása van: x1 és x2. Ha C(x) és D(x) negatívok, akkor a kisszámú együttműködő nagy büntetést kap, a nagyszámú hűtlen pedig kicsit. Ennek következtében a játék eredménye az lesz, hogy viszonylag alacsony kezdeti együttműködési arány mellett x értéke a kezdeti állapottól függetlenül az első egyensúlyi érték (x1) körül fog ingadozni az idő függvényében. Ha C(x) és D(x) pozitívak, akkor a sok együttműködő kis jutalmat kap, a kevés hűtlen viszont nagyot. E második egyensúlyi helyzet (x2) felett az eredmény egy-egy meghatározott x érték, a viszonylag magas kezdeti állapottól függően (4. ábra).
Az egyensúlyi egyenlet megoldásai az 1. ábra függvényeire x1 = 0,180, x2 = 0,695. Ennek megfelelően a 4. ábra görbéi a kezdeti együttműködési arány nagyon széles intervallumában (0-tól 0,69-ig) az 50-100. lépéstől kezdve mind az x1 érték körül ingadoznak. Ebből láthatjuk, hogy a pavlovi ágensek nem esnek teljesen bele a fogolydilemma csapdájába – szemben a racionális, azaz mindig hűtlenkedő kollegáikkal, akik a pillanatnyilag kedvezőnek tűnő, de végső soron rossz megoldást választják. Ugyanakkor jelentős együttműködési arány csak akkor tartható fenn, ha ez már a kiindulási állapotban is így van.
Más a helyzet, ha az ágensek egyrétegű sejtautomaták, vagyis csak közvetlen szomszédjaikkal vannak kölcsönhatásban. Ebben az esetben az együttműködők arányát a lépések számának (idő)függvényében az 5. ábrán láthatjuk.
Ha viszont azt feltételezzük, hogy a résztvevők mind konformisták, akkor a szimuláció azt mutatja, hogy mind az együttműködők, mind a hűtlenek egymásba ágyazódó csoportosulásokat alkotnak (6. ábra).
Autó vagy tömegközlekedés
Korunk egyik tragédiája a környezet tönkretétele a kipufogógázok által. Mivel a saját autó kényelmesebb, mint a tömegközlekedés, nehéz az embereket meggyőzni arról, hogy legalább a nagyvárosokban ne autóval menjenek munkába. Ha azonban mindenki az autót választja, akkor olyan forgalmi dugók keletkeznek, hogy senki sem tud előrejutni, kivéve az autóbuszokat, amelyeknek külön sáv áll a rendelkezésére. Ebben az esetben tehát a tömegközlekedés előnyösebb. Ezt a helyzetet szemlélteti a 7. ábra [Szilagyi 4].
A két függvény most keresztezi egymást. Sok együttműködő (kevés autó) esetén az autó a jobb, ha viszont kevés az együttműködő (sok az autó), akkor a tömegközlekedés. Ha elhelyezzük a P, R, S, T értékéket az ábrán, akkor láthatjuk, hogy ez az eset a sokszereplős gyávanyúl-dilemmának felel meg (T > S > R > P). Racionális játékosok esetén az egyensúlyi helyzet a két görbe kereszteződési pontjában alakulna ki, hiszen ettől a ponttól balra érdemesebb együttműködni, vagyis a görbén jobb felé elmozdulni, míg a kereszteződéstől jobbra a hűtlenség előnyös, tehát érdemes bal felé tartani. A szimulációk azt mutatják, hogy a valódi egyensúlyi helyzet erősen függ a résztvevők személyiségétől.
Az eredményt természetesen nagymértékben a jutalmak/büntetések mértéke határozza meg. Ezek sok tényezőtől függnek (útviszonyok, az autók, a benzin és az autóbuszjegyek ára stb.). A szimuláció azonban meg e tényezők konkrét ismerete nélkül is érdekes eredményeket mutat. Így például megállapítható, hogy a tömegközlekedés győzelméhez az szükséges, hogy a D(x) függvény előjele megváltozzék az együttműködők arányának növekedésével, vagyis az autósok csak akkor kapjanak jutalmat, ha kevesen vannak, és büntetésben részesüljenek, ha ők vannak többségben.
Lakóhelyi elkülönülés
Az amerikai társadalom egyik jelentős problémája a fajok elkülönülése. Ismeretesek a nagyvárosokban kialakult fekete gettók, de Los Angelesben olyan városrészek is vannak, ahol mindenki kizárólag spanyolul beszél.
Az elkülönülés oka a résztvevők konformizmusa. Jelentős részük elvárja, hogy a környezetükben élők között az ő fajtájukhoz tartozók legalább egy bizonyos arányban képviselve legyenek. Amennyiben ez nem teljesül, a legközelebbi olyan üresedést foglalják el, ahol kívánságuk szerinti az arány. Ennek az lesz az eredménye, hogy a 6. ábrán látható képhez hasonló elkülönülés jön létre. A szimuláció azt mutatja, hogy a kívánt arány kismértékű megváltoztatása is a kialakuló elrendeződés erős megváltozását okozza.
További lehetőségek
A sokszereplős játékelmélet a legkülönbözőbb problémák elemzésére használható. Egyes kutatók szerint [Nowak–May] arra is alkalmas, hogy az együttműködés evolúcióját tanulmányozzuk. Nagyon érdekes alakulatokat figyelhetünk meg, ha az ágenseket mohó sejtautomatáknak tekintjük. A szimuláció során kaleidoszkópszerű képek váltakoznak végtelen variációkban. Ezek különösen akkor lenyűgözőek, ha az ágensek különböző állapotait különböző színekkel szemléltetjük attól függően, hogy az ágens állapota hogyan és mikor változik meg.
A 8. ábra egy ilyen kaleidoszkóp képét mutatja fekete-fehérben az 1000. lépés után egyszerű jutalom/büntetés-függvények esetén [C(x) = x, D(x) = 1,65x], ha a kezdeti állapotban egyetlen hűtlen helyezkedik el az együttműködők tengerében. A hűtlen játékos magasabb jutalmat kap, mint társai, ezért fokozatosan megfertőzi környezetét. A kialakuló szituáció azonban annyira bonyolult, hogy az ágensek állapotai előre megjósolhatatlan módon váltakoznak az együttműködés és a hűtlenség között.
Amint láttuk, a lehetséges esetek száma végtelen, mint ahogy az élet is végtelen számú szituációt foglal magában. Ebben a rövid összefoglalóban csak a sokszereplős játékelmélet alapjainak bemutatására volt lehetőség. Vizsgálhatjuk a társadalom méretének hatását az együttműködés kialakulására, a tőzsde és egyéb piacok mozgásait, a résztvevők közötti alkudozásokat, csoportpszichológiai jelenségeket, a terrorizmus elleni harc különböző vonatkozásait, társadalmi normák kialakulását, sőt az emberi viselkedés befolyásolásának különböző módozatait vagy éppen mesterséges társadalmakat [Epstein–Axtell] is. Természetesen olyan szituációk elemzése is lehetséges, amikor a résztvevők kettőnél több lehetőség közül választhatnak.
A játékelmélet lehetővé teszi, hogy olyan társadalmi kísérleteket végezzünk, amelyeket élő emberekkel lehetetlen lenne végrehajtani. Mindezek elvégezhetők a paraméterek változtatásával. Így vizsgálhatjuk meg például, hogyan hatnak a különböző adókulcsok a gazdasági életre, a benzin ára a tömegközlekedés hatékonyságára, a büntetések mértéke a kihágások gyakoriságára, és így tovább.
A játékelmélet matematika, tehát eredeti célja nem konkrét döntési problémák megoldása volt. Mivel azonban a politika, az üzlet, a háború, sőt maga az élet is játék, ezért a biológia, közgazdaságtan, szociológia, társadalomkutatás, kül- és belpolitika, pszichológia, haditudomány, jog, sport területén megannyi olyan probléma van, amelyet a játékelmélet segítségével sikeresen lehet tanulmányozni, sőt néhányat megoldani is. Jó lenne, ha a törvényhozók és rendeletalkotók ismernék, hiszen akkor sok hibás döntés elkerülhető lenne.
Ábrák
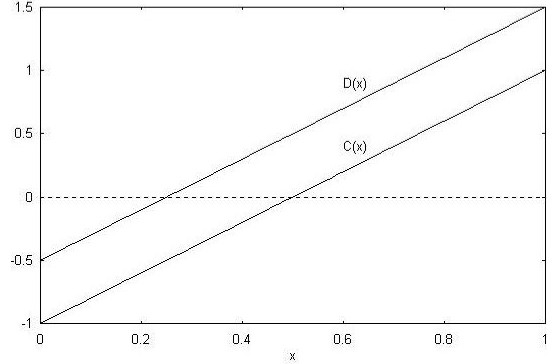
1. ábra. A legelő tragédiájának jutalom/büntetés függvényei. Az együttműködők aránya x, a függőleges irány az együttműködők (C), illetve a hűtlenek (D) jutalmát/büntetését jelöli. Ebben az esetben D(x) = 2x – 0,5 és C(x) = 2x – 1.

2. ábra. Az ágensek véletlenszerű kezdeti elhelyezkedése abban az esetben, ha a szimuláció körülbelül azonos számú együttműködővel (fekete pontok) és hűtlennel (fehér pontok) indul.
3. ábra. A pavlovi ágensek elhelyezkedése a 100. lépés után az 1. ábrán látható jutalom/büntetés függvények esetén.
4. ábra. A legelő tragédiájának időbeli lefolyása pavlovi ágensek és az 1. ábrán megadott jutalom/büntetés függvények esetén. Mindenki mindenkivel kölcsönhatásban van. Az ábrán az együttmuködők arányát látjuk a lépések számának (idő) függvényében. Az együttműködők kezdeti aránya a legfelső görbétől a legalsóig rendre 0,90, 0,80, 0,75, 0,73, 0,71, 0,69, 0,65 és 0,00.
5. ábra. A legelő tragédiájának idobeli lefolyása pavlovi ágensek és az 1. ábrán megadott jutalom/büntetés függvények esetén, ha az ágensek egyrétegű sejtautomaták. Az ábrán az együttmuködők arányát látjuk a lépések számának (idő) függvényében. Az együttműködők kezdeti aránya a legfelső görbétől a legalsóig rendre 0,90, 0,80, 0,75, 0,73, 0,71, 0,69, 0,65 és 0,00.
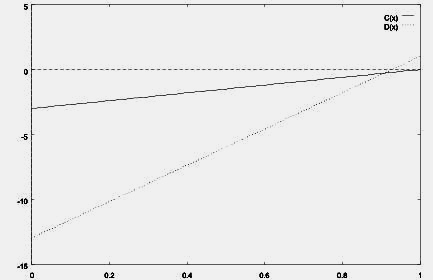
7. ábra. Az autó kontra tömegközlekedés jutalom/büntetés függvényei. A vízszintes tengelyen az együttműködők arányát, függőleges irányban az együttműködők (C), illetve a hűtlenek (D) jutalmát/büntetését jelöltük. Ebben az esetben D(x) = 14x – 13 és C(x) = 3x – 3.
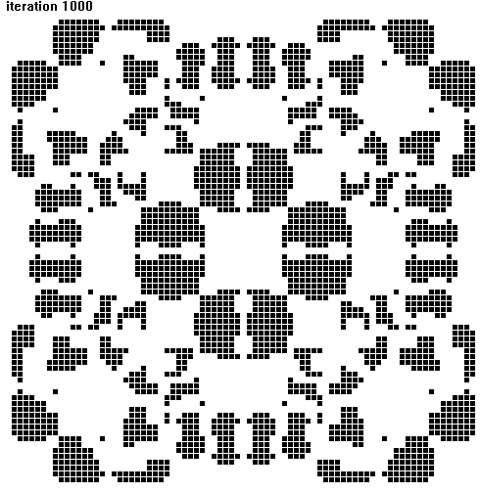
8. ábra. A kaleidoszkóp képe az 1000. lépés után nagyon egyszerű jutalom/büntetés függvények esetén (C = x, D = 1,65 x), ha a kezdeti állapotban egyetlen hűtlen helyezkedik el az együttműködők tengerében. Az ágensek mohó sejtautomaták.
Felhasznált irodalom
Axelrod, R.: The Evolution of Cooperation. New York, Basic Books, 1984.
Epstein, Joshua M. – Axtell, Robert: Growing Artificial Societies. Washington–Cambridge–London, Brookings Institution Press – MIT Press, 1996.
Gardner, Martin: Wheels, Life, and other Mathematical Amusements. New York, Freeman, 1983.
Hardin, G.: The tragedy of the Commons. Science 162, 1968. 1243–8.
Hoffmann, R.: Twenty years on: The Evolution of Cooperation revisited. Journal of Artificial Societies and Social Simulation 3, 2000. 2.
McCulloch, Warren S. – Pitts, Walter: A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biophysics 5, 1943. 115–33.
Neumann, John: Zur Theorie des Gesellschaftsspiele. Mathematische Annalen 100, 1928. 295–320.
Neumann, John – Morgenstern, Oskar: Theory of Games and Economic Behavior. Princeton, Princeton University Press, 1944.
Nowak, M. A. – May, R. M.: Evolutionary games and spatial chaos. Nature 359, 1992. 826–9.
Oldham, John M. – Morris, Lois B.: The New Personality Self-Portrait. New York, Bantam Books, 1995.
Rapoport, A. – Chammah, A. M.: Prisoner’s Dilemma. Ann Arbor, University of Michigan Press, 1965.
Rapoport, Anatol – Guyer, Melvin: A taxonomy of 2*2 games. General Systems 11, 1966. 203–14.
Szilagyi Miklos: Solutions to realistic Prisoners’ Dilemma games. Proceedings of the 2001 IEEE International Conference on Systems, Man, and Cybernetics, TA12/2, 2001. 841–6.
Szilagyi Miklos: Simulation of multi-agent Prisoners’ Dilemmas. Systems Analysis, Modelling, Simulation, Vol. 43, No. 6, 2003. 829–46.
Szilagyi Miklos: An investigation of N-person Prisoners’ Dilemmas. Complex Systems, Vol. 14, 2003. 155–74.
Szilagyi Miklos: Computer simulation of the N-person Chicken Dilemma for Pavlovian agents. Proceedings of the 11th International Symposium on Dynamic Games and Applications, 2004. 980–5.
Szilagyi Miklos – Szilagyi Zoltan: A tool for simulated social experiments. Simulation, Vol. 74, 2000. 4–10.
Szilagyi Miklos – Szilagyi Zoltan: Nontrivial solutions to the
N-person Prisoners’ Dilemma. Systems Research and Behavioral Science, Vol. 19, 2002. 281–90.
Wolfram, Stephen: A New Kind of Science. Champaign, Wolfram Media, 2002.
- A hozzászóláshoz regisztráció és belépés szükséges






Friss hozzászólások
7 év 29 hét
10 év 2 hét
10 év 6 hét
10 év 6 hét
10 év 7 hét
10 év 8 hét
10 év 8 hét
10 év 10 hét
10 év 11 hét
10 év 11 hét